Conformal vector field
A conformal vector field (often conformal Killing vector field and occasionally conformal or conformal collineation) of a Riemannian manifold 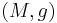 is a vector field
is a vector field  that satisfies:
that satisfies:
for some smooth real-valued function  on
on  , where
, where  denotes the Lie derivative of the metric
denotes the Lie derivative of the metric  with respect to
with respect to  . In the case that
. In the case that  is identically zero,
is identically zero,  is called a Killing vector field.
is called a Killing vector field.
